Cynthia Chung
La théorie des jeux, la théorie mathématique des jeux de stratégie, a été développée par John von Neumann en plusieurs étapes successives en 1928 et 1940-41, selon son livre "Theory of Games and Economic Behaviour" qu'il a co-écrit avec Oskar Morgenstern.
L'essentiel de la théorie est que le comportement d'un individu sera toujours motivé par la recherche d'un résultat optimal, déterminé par l'intérêt personnel. On suppose que les joueurs d'un tel jeu sont rationnels, ce qui signifie qu'ils "s'efforceront de maximiser leurs gains dans le jeu". En d'autres termes, on suppose qu'ils sont motivés par des intérêts personnels égoïstes.
Au fil des ans, d'autres contributeurs tels que John Nash (équilibre de Nash) et John Maynard Smith (stratégie évolutionniste stable) ont enrichi la théorie et nous en sommes maintenant à un point où elle est considérée par beaucoup comme un outil essentiel pour modéliser les comportements et les résultats économiques, politiques, sociologiques ou militaires, et est enseignée en tant que telle dans de nombreuses universités prestigieuses comme quelque chose d'assez gravé dans le marbre.
Mais que faire si nous avons fait une terrible erreur ?
Après tout, les théoriciens eux-mêmes reconnaissent que tout le fonctionnement de leur modèle repose sur l'hypothèse [u] que nous sommes gouvernés par un comportement égoïste rationnel, et qu'ils se sentent en confiance par rapport à cette hypothèse puisque la réalité leur a apparemment confirmé ce fait. Mais qu'en est-il si ce jeu ne reflète pas objectivement une représentation véridique de nous ? Et si ce jeu avait plutôt été utilisé comme un outil de conditionnement, une prophétie auto-réalisatrice, une boucle de rétroaction positive ?
Comment [pouvons-nous] savoir ce qui est vrai ? Comment [pouvons-nous] savoir quel genre de personne nous sommes vraiment et non pas ce que nous avons été conditionnés à penser de nous-mêmes ?
Théorie des jeux et comportement économique
Avant de pouvoir répondre à une telle question, nous devons examiner les formes de simplification et les hypothèses qui ont été utilisées par von Neumann lors de la formulation de la philosophie du modèle de la théorie des jeux. Cela peut être contre-intuitif pour certains, mais la "philosophie" ou l'"hypothèse" doit toujours précéder le modèle réel. Les variables que vous choisissez d'utiliser, les variables que vous écartez, la façon dont vous définissez les variables, la façon dont vous définissez la relation entre les variables ne sont pas définies par le modèle, mais plutôt par le créateur du modèle. Une fois le modèle créé, il peut maintenant, théoriquement, s'ajouter à cette structure de départ et imiter une version simplifiée de la réalité.
Cependant, nous devons garder à l'esprit qu'un modèle créé sur une fausse hypothèse peut toujours "fonctionner", si les variables ne sont pas trop en contradiction avec les opérations des autres variables. Un tel modèle n'est pas "conscient" qu'il n'est pas une représentation de la "réalité", et ne peut l'indiquer à son créateur. Ainsi, un modèle peut être une représentation d'une réalité simplifiée ou il peut représenter une réalité complètement artificielle.
Au début du livre de von Neumann, il passe par plusieurs mises en garde qui sont très problématiques quant à la pertinence de sa théorie, l'une d'elles étant la reconnaissance du fait qu'"il n'existe, à l'heure actuelle, aucun traitement satisfaisant de la question du comportement rationnel". Il peut, par exemple, exister plusieurs façons d'atteindre la position optimale ; elles peuvent dépendre des connaissances et de la compréhension que l'individu possède et des voies d'action qui lui sont ouvertes, car elles impliquent, comme cela doit être évident, des relations quantitatives".
Comme cela devient rapidement évident, von Neumann fait des affirmations sans fin comme celles-ci, comme si elles étaient évidentes et n'avaient donc pas besoin d'être examinées du tout. L'hypothèse selon laquelle un comportement égoïste "rationnel" sous-défini n'est que quantifiable et rien de plus, et ne tient pas compte du changement qualitatif (le pire cauchemar d'un mathématicien), prend une grande liberté en simplifiant à l'excès le comportement humain pour qu'il corresponde aux paramètres limités de son modèle. En d'autres termes, c'est tricherie. Vous manipulez les définitions et les interactions de vos variables pour les faire correspondre à une réalité artificielle de votre modèle.
Laissez-moi vous donner un exemple.
Dans le cinquième postulat d'Euclide fifth postulate, il est considéré comme une "règle" selon laquelle deux lignes parallèles ne se croiseront jamais. Euclide était vivant vers le milieu du IVe siècle avant J.-C., avant qu'Eratosthène (276-194 avant J.-C.) ne fasse sa belle et élégante découverte que la Terre était en effet incurvée et ne fasse une première mesure assez précise de la taille de la Terre.
En d'autres termes, Euclide supposait un espace géométrique linéaire sur lequel l'univers réel était censé "tenir". S'il est vrai que deux lignes parallèles ne se rencontreront jamais sur un plan bidimensionnel, elles peuvent se rencontrer sur un plan tridimensionnel.
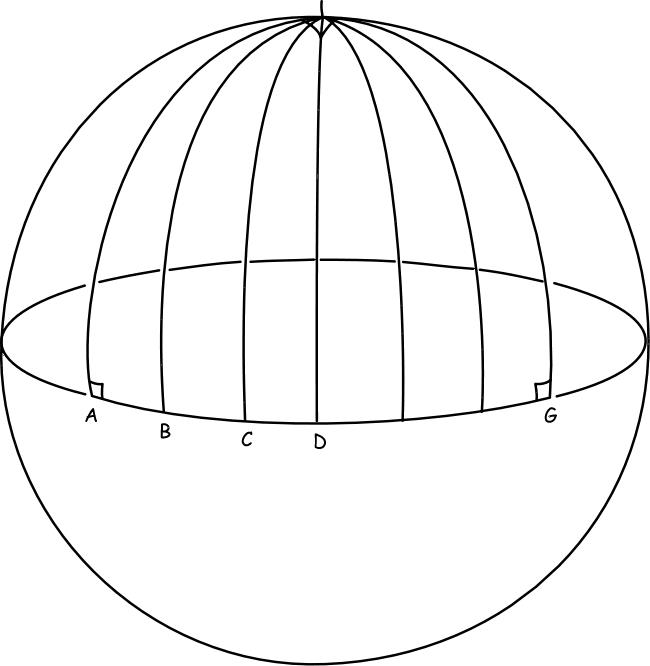
Comme on le comprend maintenant, la ligne A et la ligne G peuvent être mesurées à 90 degrés de la ligne de l'équateur et sont donc des lignes parallèles, et pourtant elles peuvent éventuellement s'interfacer l'une avec l'autre si la surface est courbée [voir image].
Le problème avec les hypothèses de tels Euclides est qu'elles ne sont finalement vraies que dans une situation artificielle et ne reflètent pas la façon dont ces choses vont interagir dans la réalité. De plus, il est impossible de prédire, à partir de la cinquième loi d'Euclide, comment deux lignes parallèles interagiraient dans un espace tridimensionnel, et encore moins dans l'espace dimensionnel n tel que décrit par le physicien Bernard Riemann.
Ironiquement, dans son livre, von Neumann compare son travail de "pionnier" dans le domaine de la théorie des jeux à ce que font les physiciens depuis des siècles, c'est-à-dire des formulations mathématiques qui représentent, bien que simplifiées, les "lois de la nature" concernant la matière et l'énergie. Cependant, von Neumann montre une fois de plus qu'il n'a aucune compréhension de ce qui constitue le fondement de ces "lois de la nature".
Dans ses Hypothèses qui reposent sur les fondements de la géométrie et autres travaux, Riemann a rigoureusement développé la notion d'un espace-temps physique anti-euclidien façonné non pas par les dimensions linéaires d'une "grille x,y,z", mais plutôt par les dimensions définies par un ensemble toujours croissant de principes physiques découverts tels que le magnétisme, la lumière, la chaleur, la gravité, le son, etc.
Selon la logique d'Euclide, on ne "voit" jamais deux lignes parallèles se croisant et il est donc insondable qu'elles ne puissent jamais se croiser. Sa "règle" était fondée sur des hypothèses communes concernant ce que nous "pensons" observer dans de tels phénomènes, mais ce n'est pas nécessairement la réalité et cela ne se traduit certainement pas par une "règle" qui régit tout.
En reconnaissant que von Neumann s'appuie lui-même largement sur ses vérités dites "évidentes" pour simplifier le comportement humain, il affirme est un résultat, il ne prouve pas l'occurrence naturelle du résultat.
L'exemple de Robinson Crusoë dans la théorie économique monétariste
Selon von Neumann, l'exemple de Robinson Crusoë a été utilisé par l'école économique autrichienne pour modéliser le comportement d'un individu en vue de maximiser les bénéfices dans un environnement (dans ce cas une île) où les ressources disponibles sont fixes et limitées.
Cela pose de nombreux problèmes, mais le plus impardonnable est l'hypothèse d'une réserve fixe, limitée et immuable de ressources à la disposition de l'individu. En d'autres termes, l'école d'économie autrichienne et von Neumann avec eux, considèrent l'île déserte de Crusoé comme le cas parfait pour un scénario de jeu à ressources limitées et à somme nulle.
Ironiquement, cette affirmation passe totalement à côté de ce qui se passe réellement dans l'histoire de Daniel Defoe de " Robinson Crusoe", et amène à se demander si ces théoriciens ont jamais lu le livre ou plutôt un synopsis de deux lignes des notes de la falaise.
Henry C. Carey, le conseiller économique de Lincoln, dirait dans son livre "Unity of Law" (1872) :
"Crusoé ayant fait un arc, avait ainsi acquis une richesse ; cette richesse se manifestant dans le pouvoir obtenu sur certaines propriétés naturelles du bois et de la fibre musculaire, lui permettant ainsi de s'assurer un approvisionnement accru en nourriture avec une dépense de travail fortement diminuée. Ayant fait un canoë, il trouva sa richesse beaucoup plus grande, sa nouvelle machine lui permettant d'obtenir encore plus de nourriture, et de matières premières pour l'habillement, à un coût d'effort personnel encore réduit. En érigeant un mât sur son canoë, il commande maintenant les services du vent, et à chaque pas dans cette direction, il se trouve à avancer, avec une rapidité sans cesse accélérée, vers la maîtrise de la nature, et vers un être de réelle richesse et de pouvoir".
Est-ce que cela ressemble à la description d'un scénario de "ressource limitée", de "jeu à somme nulle" ? En d'autres termes, où est la limite "fixée" ? La limite est constamment réajustée en fonction de ce que l'individu crée, ce qui modifie son rapport à l'"utilité" de la ressource.
Par exemple, la ressource bois, selon l'innovation de l'individu, peut être utilisée pour garder une personne au chaud et au sec, cuire de la nourriture, créer des armes, créer un abri, créer un bateau pour voyager, etc. etc.
L'existence d'un potentiel à créer compense donc tout le système de von Neumann car son système n'a aucun moyen de prédire le potentiel, c'est-à-dire les transformations qualitatives, ni la manière dont il affectera le comportement.
Si vous ne pouvez pas prédire les changements qualitatifs futurs, qui sont en cours, comme la découverte de l'électricité ou la création de plutonium et d'autres éléments transuraniens fabriqués par l'homme, ou le potentiel qui attend d'être débloqué par la très réalisable torche à plasma à fusion qui peut transformer les décharges en mines de ressources, comment pouvez-vous considérer une limite définie ou même un jeu à somme nulle comme une vérité "évidente" alors que vous ne pouvez même pas prédire quelle est la limite ?
Le supposé paradoxe du "plus grand bien pour le plus grand nombre"
Dans son livre, von Neumann parle de "le plus grand bien pour le plus grand nombre possible" comme d'une contradiction, car selon von Neumann, on ne peut pas maximiser deux ou plusieurs fonctions à la fois, que dans une économie sociale, toutes les maxima sont souhaitées en même temps par différents acteurs.
En d'autres termes, il n'y a pas de concept selon lequel il est possible de coopérer et de partager un résultat optimal, sans que celui-ci ne provienne de "votre" part, pour ainsi dire, qui a un coût d'avoir moins au lieu de plus. Il s'agit là d'une compréhension très élémentaire de l'économie, qui ne tient pas compte de la manière dont la coopération et le potentiel créatif peuvent contribuer à transformer les "biens" d'un résultat.
Par exemple, le pays A est militairement plus fort que le pays B, qui est riche en nombreuses ressources brutes. Le pays A est également plus fort politiquement que le pays B en ce sens qu'il n'y a pas d'autres pays qui interviendront probablement contre les actions du pays A s'il choisit d'envahir le pays B. Quelle ligne de conduite permettra d'obtenir le meilleur rendement pour le pays A ?
Il y a une réponse très évidente à cette question ; cependant, contrairement à ce que l'on pense généralement, elle ne donnera pas le meilleur résultat. Le meilleur résultat est plutôt de coopérer.
Il est dans l'intérêt du pays A et du pays B de partager leurs connaissances, même si le pays A possède beaucoup plus de connaissances, de sorte que le pays B développe la capacité de raffiner ses ressources brutes. Ce faisant, le pays B rapportera à long terme un plus grand rendement commercial au pays A, et le pays A n'a pas à s'inquiéter de futures représailles de la part du pays B. En développant une économie plus avancée, la richesse du commerce est accrue pour les deux pays. La coopération transforme le résultat optimal et offre un meilleur rendement.
C'est exactement le modèle qu'utilise actuellement la Chine dans sa philosophie de "coopération gagnant-gagnant", et il s'est avéré des plus efficaces malgré toutes les tentatives de le vilipender comme quelque chose de malfaisant. Plutôt que de se battre pour les ressources, il existe une coopération visant à partager la technologie, à augmenter le rendement des ressources et à partager une plus grande aubaine que celle qui existait à l'origine.
John von Neumann poursuit dans son livre, que plus le nombre d'acteurs dans le modèle est élevé, plus il est facile de prévoir le résultat, puisque l'utilisation de statistiques et de probabilités sont de meilleurs indicateurs de comportement et de performance. Comme il l'affirme :
"Lorsque le nombre de participants devient vraiment important, on peut espérer que l'influence de chaque participant particulier deviendra négligeable et que les difficultés susmentionnées pourront s'estomper et qu'une théorie plus conventionnelle deviendra possible. Ce sont là, bien entendu, les conditions classiques de la "libre concurrence"".
Il poursuit en prenant l'exemple de notre système solaire, avec ses neuf corps principaux, comme étant beaucoup plus difficile à modéliser que 10^25 particules de gaz en mouvement libre, selon la théorie des gaz, simplement en raison du nombre d'objets auxquels vous avez affaire.
C'est vraiment une affirmation remarquablement absurde, où von Neumann affirme que si le système solaire avait plus de corps majeurs en orbite à l'intérieur de celui-ci, il serait donc plus facile de le modéliser en se basant sur la probabilité.
Chaque planète de notre système solaire a une taille et un poids différents, avec un nombre de lunes différent. Chaque planète tourne autour du soleil selon des orbites elliptiques imparfaites qui changent lentement avec le temps, les planètes voyagent le long de ces orbites d'une manière non uniforme qui est observable par des mouvements rétrogrades planétaires. Le fait est que notre système solaire n'est pas un système parfaitement fermé, uniforme et cohérent dans ses actions, il y a des changements cycliques mais aussi des changements non cycliques qui se produisent. Cela est dû au fait que notre système solaire tourne autour d'un centre galactique de la Voie lactée qui se déplace lui-même selon des voies encore à découvrir au sein d'un plus grand amas de galaxies.
Par conséquent, vous ne pouvez utiliser aucune théorie des probabilités car le système est dans un état de changement non linéaire continu. Plus vous ajoutez de corps à un tel système, plus il devient complexe, et non négligeable.
Par exemple, il n'existe pas de formule simple pour identifier tous les nombres premiers, bien qu'il y en ait un nombre infini. Les nombres premiers sont le reflet d'un processus de changement non linéaire.
Une telle simplification excessive de la nature montre l'audace des hypothèses qui composent de telles formulations comme la théorie des jeux. Vous n'êtes rien d'autre qu'un avatar virtuel dans leur monde synthétique avec des limites programmées à ce que vous pouvez et ne pouvez pas faire dans le jeu qu'ils ont créé pour vous.
La théorie des jeux ne représente pas les motivations de la nature humaine, mais impose plutôt de telles limites car, comme elles se reconnaissent elles-mêmes, il est plus facile de prévoir et de contrôler les comportements égoïstes que vous avez choisis et qui sont encouragés et récompensés par des "incitations".
Il s'agit d'un système d'asservissement qui encourage ses esclaves à se battre entre eux pour des "restes de table" et à ne jamais remettre en question la main qui les retient, système qui crée une fausse rareté et favorise l'antagonisme par rapport à des facteurs de stress artificiels.
On nous apprend à ne jamais remettre en question les règles qui nous sont données dans ces scénarios de théorie des jeux, mais à réagir en conséquence à ce qui nous a été défini comme un ensemble limité d'options dans un scénario artificiel.
Le meilleur indicateur de ce fait est peut-être, ironiquement, le créateur même du dilemme du prisonnier, John Nash. Nash a reçu le prix Nobel d'économie en 1994 pour ses travaux "marquants" sur la théorie des jeux, qui ont débuté dans les années 50. Bien qu'il ne soit pas clair s'il souffrait de schizophrénie paranoïde lorsqu'il a développé l'équilibre de Nash, à partir de 1959, Nash a fait des allers-retours dans des hôpitaux psychiatriques pendant plus de neuf ans.
En 2007, il a été interviewé alors qu'il travaillait encore à Princeton. Voici son offre très désintéressée de son "éclaircissement" (ses mots) sur la théorie des jeux après plus de 50 ans de travail dans le domaine. N'oubliez pas qu'il utilise la définition du comportement rationnel selon la théorie des jeux, qui est définie comme un intérêt égoïste :
"J'ai moi-même eu quelques problèmes sur le plan psychologique ; j'ai été dans des hôpitaux psychiatriques... Je me rends compte que ce que j'avais dit à un moment donné a peut-être surestimé la rationalité... Et je ne veux pas surestimer la pensée rationnelle des humains... Les êtres humains sont beaucoup plus compliqués, l'être humain en tant qu'homme d'affaires....Le comportement humain n'est pas entièrement motivé par l'intérêt personnel de chaque humain... La théorie des jeux fonctionne en termes d'intérêt personnel, mais... certains concepts de la théorie des jeux pourraient être mal fondés. Il y a une dépendance excessive à la rationalité. C'est ce qui m'a éclairé".
L'auteur peut être contacté à cynthiachung@tutanota.com